Type of relationship in statistics crossword clue introduces a captivating realm of statistical analysis, delving into the intricacies of relationships between variables. This comprehensive guide unveils the diverse types of relationships, unraveling their characteristics and showcasing practical applications. Join us as we embark on an enlightening journey through the fascinating world of statistical relationships.

This guide offers a comprehensive exploration of types of relationships in statistics, correlation and regression, types of correlation, types of regression, and model selection and validation. Through lucid explanations and illustrative examples, it unravels the complexities of statistical relationships, empowering readers with a profound understanding of this fundamental concept.

Types of Relationships in Statistics

In statistics, relationships between variables can be classified into different types based on their characteristics. Understanding the type of relationship between variables is crucial for choosing appropriate statistical methods for analysis and interpretation.

Types of Relationships

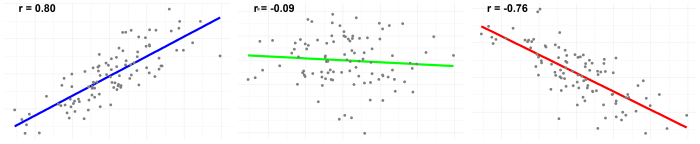
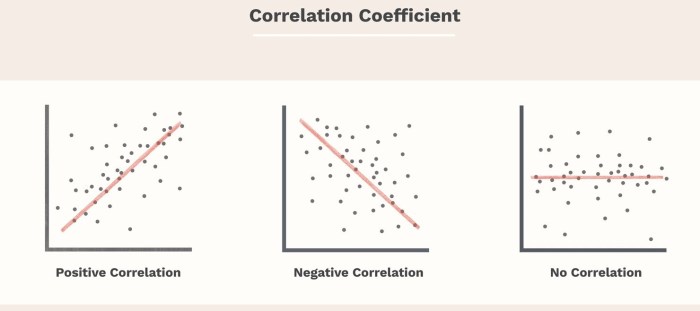
• Positive Relationship:A positive relationship exists when the values of two variables increase or decrease together. As one variable increases, the other variable also tends to increase, and vice versa.
• Negative Relationship:A negative relationship exists when the values of two variables move in opposite directions. As one variable increases, the other variable tends to decrease, and vice versa.
• Linear Relationship:A linear relationship exists when the points plotted on a scatter plot form a straight line. The relationship is described by a linear equation, y = mx + b, where m is the slope and b is the y-intercept.
• Curvilinear Relationship:A curvilinear relationship exists when the points plotted on a scatter plot do not form a straight line. The relationship is described by a non-linear equation, such as a parabola or exponential function.
• Monotonic Relationship:A monotonic relationship exists when the values of two variables always increase or decrease together. The relationship is not necessarily linear, but it does not change direction.
• Non-Monotonic Relationship:A non-monotonic relationship exists when the values of two variables do not always increase or decrease together. The relationship may change direction at some point.

Correlation and Regression

Correlation and regression are two statistical techniques used to analyze relationships between variables. Correlation measures the strength and direction of a linear relationship, while regression models the relationship between a dependent variable and one or more independent variables.

Correlation

• Measures the strength and direction of a linear relationship between two variables.
• Ranges from -1 to 1, where -1 indicates a perfect negative relationship, 0 indicates no relationship, and 1 indicates a perfect positive relationship.
• Does not imply causation.

Regression

• Models the relationship between a dependent variable and one or more independent variables.
• Uses a mathematical equation to predict the value of the dependent variable based on the values of the independent variables.
• Can be used to make predictions and test hypotheses.

Types of Correlation, Type of relationship in statistics crossword clue

• Pearson Correlation:Measures the linear relationship between two continuous variables.
• Spearman Correlation:Measures the monotonic relationship between two ordinal variables.
• Kendall Tau Correlation:Measures the monotonic relationship between two ordinal variables.
• Point-Biserial Correlation:Measures the relationship between a continuous variable and a dichotomous variable.
• Phi Coefficient:Measures the relationship between two dichotomous variables.
• Contingency Coefficient:Measures the relationship between two categorical variables.

Types of Regression

• Simple Linear Regression:Models the relationship between a dependent variable and a single independent variable.
• Multiple Linear Regression:Models the relationship between a dependent variable and two or more independent variables.
• Logistic Regression:Models the relationship between a binary dependent variable and one or more independent variables.
• Poisson Regression:Models the relationship between a count dependent variable and one or more independent variables.
• Negative Binomial Regression:Models the relationship between a count dependent variable with overdispersion and one or more independent variables.
• Cox Proportional Hazards Regression:Models the relationship between a time-to-event dependent variable and one or more independent variables.

Model Selection and Validation

Model selection and validation are important steps in statistical analysis to ensure that the chosen model is the most appropriate and accurate for the data.

Model Selection

• Involves selecting the best model from a set of candidate models.
• Uses criteria such as goodness-of-fit, parsimony, and predictive accuracy.
• Common methods include stepwise selection, forward selection, and backward selection.

Model Validation

• Involves assessing the performance of the selected model on new data.
• Uses methods such as cross-validation and holdout validation.
• Helps to prevent overfitting and ensure the model’s generalizability.

FAQ Resource: Type Of Relationship In Statistics Crossword Clue

What is the difference between correlation and regression?

Correlation measures the strength and direction of a linear relationship between two variables, while regression models the relationship between a dependent variable and one or more independent variables, allowing for predictions to be made.

What are the different types of correlation?

There are various types of correlation, including positive correlation, negative correlation, and no correlation. Positive correlation indicates a direct relationship, negative correlation indicates an inverse relationship, and no correlation indicates no linear relationship.

What are the different types of regression?

Common types of regression include linear regression, multiple regression, logistic regression, and polynomial regression. Each type is tailored to specific types of relationships and data structures.